最終更新:2024年01月30日
講義中にあった質問に(なるべく)丁寧に答えるという企画。質問していない人もよかったら確認してください。
現在の質問は 39 件です。 質問をクリックすると回答が表示されます。
応用物理I
- 重心質量って何?
-
重心の運動方程式を「 $\normalsize\displaystyle{M \vec{a} =\vec{F}}$ 」のように書いたときに $\normalsize\displaystyle{M}$ にくる慣性質量のこと。 ここで $\normalsize\displaystyle{ \vec{a} }$ は重心の加速度(これは重心の位置ベクトルを $\normalsize\displaystyle{\vec{r}_{G}}$ としたときに $\normalsize\displaystyle{\frac{d^{2}\vec{r}_{G}}{dt^{2}}}$ で定義される), $\normalsize\displaystyle{\vec{F}}$ は二体系に働く外力の合力。 二体系の場合は $\normalsize\displaystyle{M=m_{1}+m_{2}}$ で計算できる。 3体系では $\normalsize\displaystyle{M=m_{1}+m_{2}+m_{3}}$ , 一般に多体系( $\normalsize\displaystyle{n}$ 体系)では \begin{equation} M =\sum_{i=1}^{n} m_{i} \end{equation} で計算できる(考えている系に登場する質量の総和)。
- 換算質量って何?
-
二体系において一方からもう一方をみたときの 運動方程式を「 $\normalsize\displaystyle{\mu \vec{a} =\vec{f}}$ 」のように書いたときに $\normalsize\displaystyle{\mu}$ にくる慣性質量のこと。 ここで $\normalsize\displaystyle{ \vec{a} }$ は相対加速度(これは相対位置ベクトルを $\normalsize\displaystyle{ \vec{r} }$ としたときに $\normalsize\displaystyle{\frac{d^{2}\vec{r}}{dt^{2}}}$ で定義される), $\normalsize\displaystyle{ \vec{f} }$ は二体系間に働く内力。 二体系の場合は $\normalsize\displaystyle{\mu= \frac{m_{1}m_{2}}{m_{1}+m_{2}}}$ で計算できる。
例えば,同じ質量 $\normalsize\displaystyle{m}$ の二体系間に引力が働いており互いに近づく運動をしている場合, 一方からもう一方をみると2倍の加速度で近づいてくるようにみえる(想像してみて)。 働く力 $\normalsize\displaystyle{f}$ はどこからみても同じなので,加速度が増加したようにみえるということは, あたかも質量が軽くなった物体の運動と同じにみえるということ。 この質量逓減の効果を直接計算する式が先の計算式。 例の同質量の二体系の場合は換算質量は半分になる。
(問) 三体系以上の場合の換算質量ってどうなるんだろう?
- 板の重心はどこ?
-
板が「一様」な場合は板の中心。一様とは,質量密度にムラがなく,一定ということ。
板の重心位置の求め方
板の質量を $\normalsize\displaystyle{m}$ ,仮想的に長さ $\normalsize\displaystyle{L}$ の一次元的なものとする場合の重心の求め方は以下のようにする。 $\normalsize\displaystyle{x}$ 軸上に沿って板を置いて,中心を原点にとる。 一様な場合は質量密度は \begin{equation} \rho =\frac{m}{L} \quad \mathrm{[kg/m]} \end{equation} であり一定(板の場所によらない)。 質量密度から \begin{equation} \int_{-\frac{L}{2}}^{\frac{L}{2}} \rho \, dx = \frac{m}{L}\int_{-\frac{L}{2}}^{\frac{L}{2}}dx = \frac{m}{L} [x]_{-\frac{L}{2}}^{\frac{L}{2}} =\frac{m}{L} \times L =m \end{equation} のように質量を計算できる。「密度を全部足す」という意味。 3次元的に広がっていてかつ連続的な物体の重心の定義は,一般に \begin{equation} \vec{r}_{G}= \iiint \rho (\vec{r})\vec{r} \; dV \end{equation} で与えられる。「位置ごとに密度の重みを考慮して平均をとる」という意味。
この重心定義を一次元の板に適用するならば \begin{equation} x_{G}=\int_{-\frac{L}{2}}^{\frac{L}{2}} \rho \;\red{x} \;dx =\frac{m}{L} \left [x^{2} \right ]_{-\frac{L}{2}}^{\frac{L}{2}} =\frac{m}{L}\times 0 =0 \end{equation} よって板の中心がそのまま重心位置。
- 床の上に置いた板の上を歩くとどうして板が動くの?
-
ふつうはたぶん動かない。
しかし,床と板の間に摩擦がなく,歩いている人と板の間には摩擦がある場合は, 板が動く。 これは,人と板の間に働く摩擦力は「内力」であり, 人が板上のどこに移動しようと 人と板の二体系の重心は動かないということによる帰結(運動方程式を解いた結果ともいえる)。 つまり,人が板の上を移動したとき,重心位置を不変とするために, 板は逆に動かないといけない。 いわゆる反動。物理っぽくいうと「運動量保存則」
板の移動距離の求め方
人の重心位置は人がいる所。これを $\normalsize\displaystyle{\vec{r}_{1}}$ とする。 板の重心位置は,板が「一様」な場合は板の中心。そこに質点があるのと同じ。 これを $\normalsize\displaystyle{\vec{r}_{2}}$ とする。すると,はじめの二体系の重心位置は \begin{equation} \vec{r}_{G}=\frac{m_{1}\vec{r}_{1} +m_{2}\vec{r}_{2}}{m_{1}+m_{2}} \end{equation} 人が移動したあとの人がいる所を $\normalsize\displaystyle{\vec{r}_{1}\,'}$ とし,そのときの 板の重心位置を $\normalsize\displaystyle{\vec{r}_{2}\,'}$ とすれば,そのときの二体系の重心位置は \begin{equation} {\vec{r}_{G}}\,'=\frac{m_{1}\vec{r}_{1}\,'+m_{2}\vec{r}_{2}\,'}{m_{1}+m_{2}} \end{equation} しかし,重心位置が不変の場合は \begin{equation} \vec{r}_{G}=\vec{r}_{G}\,' \end{equation} 人が距離〇〇だけ移動したとき,板が△△だけ移動した(未知数 $\normalsize\displaystyle{x}$ とする)と考えて,この重心位置が不変の 方程式をたててそれを解けば $\normalsize\displaystyle{x}$ が求まる。
物体の運動が一次元的な場合は,ベクトルの1成分で表現が可能なので,わざわざ文字上に 矢印をつけなくてもよい(つけてはイケナイ)。
この例は,頭を横にして,かつ勝手に想像を膨らませると,ガス噴射でロケットが飛んでいく原理と同じ。
- 床の上に置いた板の上を歩いたときの板の移動距離は?
-
質量 $\normalsize\displaystyle{M}$ ,長さ $\normalsize\displaystyle{L}$ の板を $\normalsize\displaystyle{x}$ 軸に置く。板の左端を座標原点とし,始めそこに質量 $\normalsize\displaystyle{m}$ の人がいて,人は $\normalsize\displaystyle{x}$ 軸正の方向に向かって板の右端まで歩くとする。 そして,歩き終えたときの板の左端の位置を $\normalsize\displaystyle{x}$ とする。
(1) 始めの人と板の二体系の重心の位置は \begin{equation} x_{G} =\frac{m \times 0 + M \times \frac{L}{2}}{m +M} \end{equation} (2) 終わりの人と板の二体系の重心の位置は \begin{equation} x_{G}'=\frac{m \times (L-x) +M \times (\frac{L}{2}-x)}{m +M} \end{equation} 以上の二体系に外力が働かない場合は重心の位置は変わらないので \begin{equation} x_{G} =x_{G}' \end{equation} つまり \begin{equation} \frac{m \times 0 + M \times \frac{L}{2}}{m +M} = \frac{m \times (L-x) +M \times (\frac{L}{2}-x)}{m +M} \end{equation} 整理すると \begin{equation} M \frac{L}{2} = m (L-x) +M (\frac{L}{2}-x) \end{equation} これを $\normalsize\displaystyle{x}$ について解けば,それが板の移動した距離。
- 作用反作用の力って物体が接してなくても働くの?
-
接していれば当然働くが離れていても働く力がある。
(例) 万有引力,電気的クーロン力など
ボールがポトッと落下するのも,そこだけみると重力が「外力」のように働いた状況であるが, 宇宙からみれば地球とボールが互いに万有引力の力(これは「内力」で作用反作用の力)で引きあっているだけ。 ちなみに接しているときに働くようにみえる力も, 拡大してみれば物体の原子間に働く電気的クーロン力の重ね合わせ。
- ナブラ $\normalsize\displaystyle{\nabla}$ って何?
-
ベクトル型の微分演算子。位置エネルギーから保存力を計算するときに登場する。
と,その前に復習。
(問) 位置エネルギーが $\normalsize\displaystyle{x}$ の関数として \begin{equation} U(x) =\frac{1}{2} kx^{2} \end{equation} と与えられるとき, $\normalsize\displaystyle{x}$ 方向に働く力はいくらか。
(答え) 微分してマイナスを掛ける。 \begin{equation} F(x) = -\frac{d U(x)}{dx} =-kx \end{equation} でこれは弾性力におけるフックの法則。力は $\normalsize\displaystyle{x}$ 軸に沿っていて常に原点の向き。 このように導出できる力を「保存力」という。
以上を踏まえて次の問い。
(問) 位置エネルギーが $\normalsize\displaystyle{r=\sqrt{x^{2}+y^{2}+z^{2}}}$ の関数として $\normalsize\displaystyle{U(r)}$ と与えられるとき, 位置 $\normalsize\displaystyle{\vec{r}=(x,y,z)}$ における $\normalsize\displaystyle{x}$ , $\normalsize\displaystyle{y}$ , $\normalsize\displaystyle{z}$ 方向に働く力はそれぞれいくらか。
(答え) \begin{equation} \vec{F}(\vec{r}) =(F_{x}(\vec{r}),F_{y}(\vec{r}),F_{z}(\vec{r}))= - \left ( \frac{\del}{\del x},\frac{\del}{\del y},\frac{\del}{\del z} \right ) U(r) \end{equation} で,ここで登場した \begin{equation} \left ( \frac{\del}{\del x},\frac{\del}{\del y},\frac{\del}{\del z} \right ) \end{equation} を $\normalsize\displaystyle{\nabla}$ と書く。「ナブラ演算子」という。 これを使うと保存力と位置エネルギーの関係を \begin{equation} \vec{F} (\vec{r}) = -\nabla U(r) \end{equation} のように簡潔に書ける。便利?
- $\normalsize\displaystyle{r =\sqrt{x^{2}+y^{2}+z^{2}}}$ のとき $\normalsize\displaystyle{\nabla U(r) }$ はどうやって計算するの?
-
\begin{eqnarray} \frac{\del U(r)}{\del x} &=& \frac{d U(r)}{dr}\frac{\del r}{\del x} \nn\\ &=& \frac{d U(r)}{dr}\frac{\del}{\del x} (x^{2}+y^{2}+z^{2})^{\frac{1}{2}}\nn\\ &=& \frac{d U(r)}{dr} \frac{1}{2} (x^{2}+y^{2}+z^{2})^{-\frac{1}{2}} \cdot 2x\nn\\ &=& \frac{d U(r)}{dr} \frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}}\nn\\ &=& \frac{d U(r)}{dr}\frac{x}{r} \end{eqnarray} 同様に \begin{equation} \frac{\del U(r)}{\del y} = \frac{d U(r)}{dr} \frac{y}{r},\quad \frac{\del U(r)}{\del z} = \frac{d U(r)}{dr}\frac{z}{r} \end{equation} よって \begin{equation} \nabla U(r) = \frac{d U(r)}{dr} \left (\frac{x}{r}, \frac{y}{r}, \frac{z}{r} \right ) =\frac{d U(r)}{dr} \frac{\vec{r}}{r} \end{equation} 常微分 $\normalsize\displaystyle{d}$ と 偏微分 $\normalsize\displaystyle{\del}$ の記号の違いに注意。
- 2物体の相対運動の運動方程式はどっちの物体の視点から見ても同じなの?
-
計算してみればよい。
外力が無く,内力が位置エネルギー $\normalsize\displaystyle{U(r=|\vec{r}_{1}-\vec{r}_{2}|) }$ から \begin{equation} \vec{f}_{12} =-\nabla_{1}U(r) \end{equation} \begin{equation} \vec{f}_{21} =-\nabla_{2}U(r) = \nabla_{1}U(r) = -\vec{f}_{12} \end{equation} によって導かれる保存力であるとすると \begin{equation} \vec{f}_{12} = -\frac{d U(r)}{dr}\frac{\vec{r}_{1} - \vec{r}_{2} }{r} \end{equation} ここで \begin{equation} \nabla_{1}=\left (\frac{\del}{\del x_{1}}, \frac{\del}{\del y_{1}}, \frac{\del}{\del z_{1}} \right ) \end{equation} \begin{equation} \nabla_{2}=\left (\frac{\del}{\del x_{2}}, \frac{\del}{\del y_{2}}, \frac{\del}{\del z_{2}} \right ) \end{equation} \begin{equation} r =|\vec{r}_{1}-\vec{r}_{2}|=\sqrt{(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}} \end{equation} 物体1の運動方程式は \begin{equation} m_{1} \frac{d^{2} \vec{r}_{1}}{dt^{2}} =\vec{f}_{12} \end{equation} 物体2の運動方程式は \begin{equation} m_{2} \frac{d^{2} \vec{r}_{2}}{dt^{2}} =\vec{f}_{21}= -\vec{f}_{12} \end{equation} それぞれの運動方程式を質量 $\normalsize\displaystyle{m_{1}}$ と $\normalsize\displaystyle{m_{2}}$ で割って引き算すると \begin{equation} \frac{d^{2} (\vec{r}_{1}-\vec{r}_{2})}{dt^{2}} =\left (\frac{1}{m_{1}} +\frac{1}{m_{2}} \right ) \vec{f}_{12} =\frac{1}{\mu} \vec{f}_{12} =- \frac{1}{\mu} \frac{d U(r)}{dr}\frac{\vec{r}_{1} - \vec{r}_{2} }{r} \end{equation} (1) 相対位置ベクトルを $\normalsize\displaystyle{\vec{r}=\vec{r}_{1}-\vec{r}_{2}}$ で定義する場合(2から1を見る)の運動方程式は \begin{equation} \mu \frac{d^{2} \vec{r}}{dt^{2}} = -\frac{d U(r)}{dr}\frac{\vec{r}}{r} \end{equation} (2) 相対位置ベクトルを $\normalsize\displaystyle{\vec{r}=\vec{r}_{2}-\vec{r}_{1}}$ で定義する場合(1から2を見る)の運動方程式は \begin{equation} - \mu \frac{d^{2} \vec{r}}{dt^{2}} = +\frac{d U(r)}{dr}\frac{\vec{r}}{r} \end{equation} つまり \begin{equation} \mu \frac{d^{2} \vec{r}}{dt^{2}} = -\frac{d U(r)}{dr}\frac{\vec{r}}{r} \end{equation} 結論:ベクトルで書いた相対運動の運動方程式は同じ形になる
- 等速円運動ではなぜ角加速度は0なの?
-
回転角を $\normalsize\displaystyle{\theta}$ とすると,角加速度の定義は \begin{equation} \alpha = \frac{ d^{2} \theta }{ dt^{2} } \quad \mathrm{[rad/s^{2}]} \end{equation} $\normalsize\displaystyle{\theta}$ が増える向きを正とすると, $\normalsize\displaystyle{\alpha}$ が正の場合,回転速度が時間ともに増大し,負であると, 回転速度が減少する(その効果が続く場合は,いずれ回転が止まり,逆回転を始める)。一方, $\normalsize\displaystyle{\theta}$ が増える向きを負とした場合は,以上の逆のことが起こる。 そして, $\normalsize\displaystyle{\alpha =0}$ の場合は,回転速度は変化せず,もともと回転していなければ,止まったままで, 回転していたら,そのまま同じ回転速度で回転が継続する。 等速円運動は,その名前の定義からして,回転速度が一定,かつ,回転半径も一定なので, $\normalsize\displaystyle{\alpha =0}$ となる。
- 電子の角運動量の下限値 $\normalsize\displaystyle{\frac{h}{2\pi}}$ の $\normalsize\displaystyle{h}$ って何者?
-
物理定数 \begin{equation} h =6.62607015 \times 10^{-34}\;\mathrm{[J \cdot s]} \end{equation} をプランク定数という。 量子力学の創始者の一人であるドイツ人物理学者マックス・プランクにちなむ。 ちなみに \begin{equation} \hbar = \frac{h}{2\pi} =1.054571817 \times 10^{-34}\;\mathrm{[J \cdot s]} \end{equation} をディラック定数という(エイチバーと読む)。イギリス人物理学者ポール・ディラックにちなむ。
- ベクトルの外積の計算方法は?
-
\begin{eqnarray} \vec{a} \times \vec{b} &=& \left | \begin{matrix} \vec{e}_{x} & \vec{e}_{y} &\vec{e}_{z}\\ a_{x} & a_{y} &a_{z} \\ b_{x} & b_{y} &b_{z}\\ \end{matrix} \right | \nn\\ &=& \vec{e}_{x} \left | \begin{matrix} a_{y} &a_{z} \\ b_{y} &b_{z}\\ \end{matrix} \right | + \vec{e}_{y} \left | \begin{matrix} a_{z} &a_{x} \\ b_{z} &b_{x}\\ \end{matrix} \right | + \vec{e}_{z} \left | \begin{matrix} a_{x} &a_{y} \\ b_{x} &b_{y}\\ \end{matrix} \right | \nn\\ &=& (a_{y} b_{z} - a_{z} b_{y} )\vec{e}_{x} + (a_{z}b_{x} -a_{x} b_{z})\vec{e}_{y} + (a_{x}b_{y} -a_{y} b_{x})\vec{e}_{z} \end{eqnarray}
- $\normalsize\displaystyle{\vec{a} \cdot \vec{a} \times \vec{b}}$ はどうやって計算するの?
-
計算の順序は,外積が先,内積は後 \begin{eqnarray} \vec{a} \cdot \vec{a} \times \vec{b} &=& ( a_{x} \vec{e}_{x} + a_{y}\vec{e}_{y} + a_{z}\vec{e}_{z} ) \cdot \{ (a_{y} b_{z} - a_{z} b_{y} )\vec{e}_{x} + (a_{z}b_{x} -a_{x} b_{z})\vec{e}_{y} + (a_{x}b_{y} -a_{y} b_{x})\vec{e}_{z} \} \nn\\ &=& a_{x} (a_{y} b_{z} - a_{z} b_{y} ) +a_{y}(a_{z}b_{x} -a_{x} b_{z})+a_{z}(a_{x}b_{y} -a_{y} b_{x})\nn\\ &=& 0 \end{eqnarray} 以上の計算は \begin{eqnarray} \vec{a}\cdot \vec{a} \times \vec{b} &=& \left | \begin{matrix} a_{x} & a_{y} &a_{z}\\ a_{x} & a_{y} &a_{z}\\ b_{x} & b_{y} &b_{z}\\ \end{matrix} \right | \end{eqnarray} を計算するのと同じで,同じ $\normalsize\displaystyle{a}$ の行があるので0。 ちなみに同様に \begin{eqnarray} \vec{b} \cdot \vec{a} \times \vec{b} &=& ( b_{x} \vec{e}_{x} + b_{y}\vec{e}_{y} + b_{z}\vec{e}_{z} ) \cdot \{ (a_{y} b_{z} - a_{z} b_{y} )\vec{e}_{x} + (a_{z}b_{x} -a_{x} b_{z})\vec{e}_{y} + (a_{x}b_{y} -a_{y} b_{x})\vec{e}_{z} \} \nn\\ &=& b_{x} (a_{y} b_{z} - a_{z} b_{y} ) +b_{y}(a_{z}b_{x} -a_{x} b_{z})+b_{z}(a_{x}b_{y} -a_{y} b_{x})\nn\\ &=& 0 \end{eqnarray} よって「 $\normalsize\displaystyle{\vec{a} \perp\vec{a} \times \vec{b} }$ 」かつ「 $\normalsize\displaystyle{\vec{b} \perp\vec{a} \times \vec{b} }$ 」である。
- 等速円運動の向心加速度はなぜ $\normalsize\displaystyle{\frac{v^{2}}{r}}$ なの?
-
向心加速度とは円運動の中心を向いた加速度。 中心向きに引かれることにより,円運動が可能となる。 力学Iの教科書の p.121 をみよ。
で,それを確認の後, 力学IIの範囲での説明としては,以下のような導出もある。前提知識は微分。 比較してみるとよい。
等速円運動のときの物体の位置座標は時刻 $\normalsize\displaystyle{t}$ を変数として, \begin{equation} \vec{r}(t)=(x,y)= (r \cos \omega t, r\sin\omega t) \end{equation} と書ける。ここで $\normalsize\displaystyle{r}$ は半径。 $\normalsize\displaystyle{\omega}$ は角速度。 つまり, $\normalsize\displaystyle{\theta = \omega t}$ が回転角度。 $\normalsize\displaystyle{\theta}$ が $\normalsize\displaystyle{2\pi}$ となる時間が回転周期でこれを $\normalsize\displaystyle{T}$ とすれば, \begin{equation} T=\frac{2\pi}{\omega} \end{equation} 物体の運動距離は円周そのものなので「速さ$\times$時間$=$道のり」より \begin{equation} vT=2\pi r \end{equation} つまり回転周期は \begin{equation} T=\frac{2\pi r}{v} \end{equation} とも書ける。したがって速度と角速度との関係は \begin{equation} \frac{2\pi r}{v} = \frac{2\pi}{\omega} \end{equation} より \begin{equation} \red{v= r \omega} \end{equation} ここまで押さえた上で,物体の速度を微分で計算すると \begin{equation} \frac{d\vec{r}}{dt}= (\frac{dx}{dt},\frac{dy}{dt}) =(-r\omega \sin \omega t, r\omega \cos \omega t) =(-v \sin \omega t, v\cos \omega t) \end{equation} さらに加速度は \begin{equation} \frac{d^{2}\vec{r}}{dt^{2}}=(\frac{d^{2}x}{dt^{2}},\frac{d^{2}y}{dt^{2}}) =(-r\omega^{2} \cos \omega t, -r\omega^{2} \sin \omega t) =- \omega^{2} (r \cos \omega t, r\sin\omega t)= - \omega^{2} \vec{r} \end{equation} これは $\normalsize\displaystyle{\vec{r}}$ に比例していて,しかも負なので,中心を向いている。 よって,これは向心加速度。 大きさだけを抽出すると \begin{equation} \left |\frac{d^{2}\vec{r}}{dt^{2}} \right | =|- \omega^{2} \vec{r}\,| = \omega^{2} |\vec{r}| = \omega^{2} r\quad\quad\mbox{(これも覚えておくとよい)} \end{equation} これに $\normalsize\displaystyle{v=r\omega}$ の関係を代入すれば \begin{equation} \left |\frac{d^{2}\vec{r}}{dt^{2}} \right | = (\frac{v}{r})^{2}r =\frac{v^{2}}{r}\quad\quad\fbox{証明終わり} \end{equation}
- 棒を傾けて回転させたときの慣性モーメントって?
-
棒の中心を原点に置いたときに回転軸と棒が角度 $\normalsize\displaystyle{\theta}$ をなしているとき, 棒上の任意の位置 $\normalsize\displaystyle{x}$ に対して 回転軸までの距離は $\normalsize\displaystyle{x \sin \theta}$ で与えられるので \begin{equation} I = \int (dm) (x \sin \theta)^{2} \end{equation} これを適切な積分範囲で定積分すればよい。 質量 $\normalsize\displaystyle{m}$ で長さ $\normalsize\displaystyle{l}$ の一様な棒の場合の質量要素は $\normalsize\displaystyle{dm=\rho dx =\frac{m}{l}dx}$ である。
- 半円板の重心って?
-
質量 $\normalsize\displaystyle{m}$ ,半径 $\normalsize\displaystyle{a}$ の一様な半円板の密度は $\normalsize\displaystyle{\rho= \frac{m}{\frac{1}{2}\pi a^{2}}}$ ,これを踏まえて \begin{equation} \vec{r}_{G}=\frac{1}{m}\int \rho \; \vec{r} dV \end{equation} を計算する。一様なので $\normalsize\displaystyle{\rho}$ は定数。 計算は極座標を用いるのが簡単。 面上の位置ベクトルを $\normalsize\displaystyle{\vec{r}=(x,y)=(r\cos \theta, r \sin \theta)}$ , 積分要素が $\normalsize\displaystyle{dV \to dS =rdr d\theta}$ となることを考慮すると \begin{eqnarray} \vec{r}_{G}&=& (x_{G},y_{G}) \nn\\ &=& \frac{1}{m} \iint \frac{m}{\frac{1}{2}\pi a^{2}} (x,y) dS \nn\\ &=& \frac{1}{m} \int_{0}^{a}rdr \int_{0}^{\pi}d\theta \; \rho \; ( r\cos\theta, r\sin \theta) \end{eqnarray} これを成分ごとに計算すればよい。 直感的に $\normalsize\displaystyle{x_{G}=0}$ であるが,これも上式を計算すると確認できる。
- 定滑車の角加速度はなぜ $\normalsize\displaystyle{a/R}$ なの?
-
滑車が角度 $\normalsize\displaystyle{\theta}$ だけ回転したときの回転分の弧の長さは $\normalsize\displaystyle{x =R \theta}$ で,これはおもりが落下した距離に等しい。 おもりの並進運動の速度は $\normalsize\displaystyle{v= \frac{dx}{dt} =R\frac{d\theta}{d t} =R\omega}$ , 加速度は $\normalsize\displaystyle{a =\frac{d^{2}x}{dt^{2}} =R\frac{d^{2}\theta}{d t^{2}} =R\alpha}$ となるので, $\normalsize\displaystyle{\alpha =\frac{a}{R}}$ の関係が導かれる。
- ブレーキをかけたときのタイヤの回転数は?
-
ブレーキによる抵抗力がタイヤの縁に作用していて大きさが一定の場合とする。 この場合は角加速度が一定なので「等角加速度回転運動」の式を用いて計算できる。 \begin{eqnarray} && \theta = \omega_{0}t +\frac{1}{2}\alpha t^{2}\\ && \omega =\omega_{0} + \alpha t \\ && \omega^{2} -\omega_{0}^{2} =2 \alpha \theta \end{eqnarray} 最初の二式は「等加速度運動」の「変位と時間の関係式 $\normalsize\displaystyle{x=v_{0}t+\frac{1}{2}at^{2}}$ 」 および「速度と時間の関係式 $\normalsize\displaystyle{v=v_{0}+at}$ 」 を回転半径 $\normalsize\displaystyle{R}$ で割ったもの, 最後の式は「速度と変位の関係式 $\normalsize\displaystyle{v^{2}-v_{0}^{2}=2ax}$ 」 を $\normalsize\displaystyle{R^{2}}$ で割ったものになっている。
一方,仕事と運動エネルギーの変化の観点から,次のように考えることも可能。
- タイヤのふちに働く抵抗力がする仕事はいくらか?
仕事とは力と距離の積。そして,距離とはタイヤの回転数と円周の積。 - その仕事によってタイヤの運動エネルギーは最終的にいくらになるか?
止まったときはゼロ。
こんな感じの式になる。 \begin{equation} W = - f' x = -f' (2 \pi R \cdot N) =0-\frac{1}{2}I \omega_{0}^{2}\;,\quad I=\frac{1}{2}MR^{2} \end{equation}
- タイヤのふちに働く抵抗力がする仕事はいくらか?
- ベクトルを回転させるとどんなベクトルになる?
-
位置ベクトル \begin{equation} \vec{r}=(x,y)=x\vec{e}_{x}+y\vec{e}_{y} \end{equation} を原点を中心として「反時計まわり」に角度 $\normalsize\displaystyle{\theta}$ だけ回転させると \begin{equation} \vec{r}\,'= (x',y')=x'\vec{e}_{x}+y'\vec{e}_{y} \end{equation} となる。このとき, \begin{equation} \left ( \begin{matrix} x'\\y' \end{matrix} \right ) = \left ( \begin{matrix} \cos\theta & -\sin \theta \\ \sin \theta & \cos\theta \end{matrix} \right ) \left ( \begin{matrix} x\\y \end{matrix} \right ) = \left ( \begin{matrix} x \cos\theta -y \sin \theta\\ x \sin \theta +y \cos\theta \end{matrix} \right ) \end{equation} の関係がある(一次変換)。 回転なので,ベクトルの長さは不変。
(証明) \begin{eqnarray} {x'\,}^{2}+{y'\,}^{2} &=& (x \cos\theta -y \sin \theta)^{2} +(x \sin \theta +y \cos\theta)^{2} \nn\\ &=& (x^{2} \cos^{2}\theta-2xy \cos\theta\sin \theta +y^{2 }\sin^{2} \theta)\nn\\ && +(x^{2} \sin^{2}\theta-2xy\sin \theta \cos\theta +y^{2 }\cos^{2} \theta )\nn\\ &=& (x^{2} +y^{2}) (\underbrace{\cos^{2}\theta + \sin^{2} \theta}_{=1})\nn\\ &=& x^{2} +y^{2} \end{eqnarray} 回転で長さが変わらないことは,回転行列の「行列式」が1であることから保証されている。 \begin{equation} \left | \begin{matrix} \cos\theta & -\sin \theta \\ \sin \theta & \cos\theta \end{matrix} \right | =\cos^{2}\theta +\sin^{2}\theta =1 \end{equation} (回転の具体例)
例えば \begin{equation} \vec{r}=(x,y)=(1,0) =\vec{e}_{x} \end{equation} を90°反時計まわりに回転させると \begin{equation} \vec{r}\,'=(0,1)=\vec{e}_{y} \end{equation} になるのは想像がつくはず。 それを踏まえて,計算で確認。 \begin{equation} \left ( \begin{matrix} x'\\y' \end{matrix} \right ) = \left ( \begin{matrix} \cos 90^{\circ} & -\sin 90^{\circ} \\ \sin 90^{\circ} & \cos 90^{\circ} \end{matrix} \right ) \left ( \begin{matrix} 1\\0 \end{matrix} \right ) = \left ( \begin{matrix} 0 & -1\\ 1 & 0 \end{matrix} \right ) \left ( \begin{matrix} 1\\0 \end{matrix} \right ) = \left ( \begin{matrix} 0\\1 \end{matrix} \right ) \end{equation} 予想通り。なお「時計まわり」に回転させたい場合は,回転行列の「逆行列」 \begin{equation} \left ( \begin{matrix} \cos\theta & -\sin \theta \\ \sin \theta & \cos\theta \end{matrix} \right )^{-1} = \left ( \begin{matrix} \cos\theta & \sin \theta \\ \red{-}\sin \theta & \cos\theta \end{matrix} \right ) \end{equation} を使えばよい。
実際のところ,角度 $\normalsize\displaystyle{\theta}$ だけ回転させて,ついで,角度 $\normalsize\displaystyle{-\theta}$ だけ回転させたら元に戻るはず。 \begin{equation} \left ( \begin{matrix} x'\\y' \end{matrix} \right ) = \left ( \begin{matrix} \cos\theta & \sin \theta \\ \red{-}\sin \theta & \cos\theta \end{matrix} \right ) \left ( \begin{matrix} \cos\theta & -\sin \theta \\ \sin \theta & \cos\theta \end{matrix} \right ) \left ( \begin{matrix} x\\y \end{matrix} \right ) = \left ( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right ) \left ( \begin{matrix} x\\y \end{matrix} \right ) = \left ( \begin{matrix} x\\y \end{matrix} \right ) \end{equation}
- 中心力だと角運動量が保存するって本当?
-
証明のヒント: \begin{equation} r^{2}\dot{\theta}=\mbox{定数} \end{equation} であることを示す。定数とは時間的に変化しないという意味。
定数かどうかを判定するには時間で微分してみればよい。というわけで早速計算すると \begin{eqnarray} \frac{d}{dt}( r^{2}\dot{\theta} ) &=& (\frac{d}{dt}r^{2})\dot{\theta} + r^{2}(\frac{d}{dt}\dot{\theta})\nn\\ &=& (\red{\frac{dr}{dt}\frac{d}{dr}r^{2}})\dot{\theta} + r^{2}(\frac{d}{dt}\dot{\theta})\nn\\ &=& \frac{dr}{dt}(2r)\dot{\theta} + r^{2}(\frac{d}{dt}\dot{\theta})\nn\\ &=& 2 r\dot{r}\dot{\theta} + r^{2}\ddot{\theta}\nn\\ &=& r (2 \dot{r}\dot{\theta} +r \ddot{\theta}) \end{eqnarray} となる。ここで, $\normalsize\displaystyle{r}$ も $\normalsize\displaystyle{\dot{\theta}}$ も,ともに時間の関数となっているので しっかりと最後まで微分をする必要がある。特に赤字のところ。 それで,この計算から \begin{equation} \frac{1}{r}\frac{d}{dt}( r^{2}\dot{\theta} )= 2 \dot{r}\dot{\theta} +r \ddot{\theta} \end{equation} という関係があることがわかる。ここで右辺は角度方向の加速度で,力が中心力( $\normalsize\displaystyle{-\vec{e}_{r}}$ 方向)の場合は,これはゼロ。 よって \begin{equation} \frac{1}{r}\frac{d}{dt}( r^{2}\dot{\theta} )= 0 \end{equation} 両辺に $\normalsize\displaystyle{r}$ をかけてもゼロ。つまり, \begin{equation} r^{2}\dot{\theta}=\mbox{定数} \end{equation} となることが示せた(定数を微分したらゼロ)。 ここまで示せると,これに定数の換算質量 $\normalsize\displaystyle{\mu}$ をかけても,やっぱり定数となるので \begin{equation} \mu r^{2}\dot{\theta}=\mbox{定数} \end{equation} そしてこれをよくみると,この定数は回転半径と接線方向の相対運動量の積で定義される「相対角運動量」になっている。 \begin{equation} L = \mu r^{2}\dot{\theta} = r (\mu r \dot{\theta}) = r (\mu v_{\theta} ) =\mbox{定数} \end{equation} ここで $\normalsize\displaystyle{v_{\theta} =r \dot{\theta} =r\omega}$ は速度の $\normalsize\displaystyle{\theta}$ 方向の成分。 したがって,角運動量が一定,つまり角運動量保存則が成立することがわかる。
ちなみに中心力は,位置エネルギー $\normalsize\displaystyle{U}$ が距離 $\normalsize\displaystyle{r}$ だけの関数の場合に導かれる。 \begin{equation} \vec{f} = -\nabla U (r) = - \frac{dU(r)}{dr} \frac{\vec{r}}{r} =f(r) \vec{e}_{r} \end{equation} 中心力のときは $\normalsize\displaystyle{f(r)<0}$ となるので, 力の向きは $\normalsize\displaystyle{-\vec{e}_{r}}$ 方向,つまり中心を向く。 このような力に対しては,一般的に相対角運動量 $\normalsize\displaystyle{\vec{L}=\vec{r} \times \vec{p}}$ の時間変化は, $\normalsize\displaystyle{\vec{f}=\frac{d\vec{p}}{dt}}$ として \begin{equation} \frac{d\vec{L}}{dt} =\vec{r} \times \vec{f} = \vec{r} \times (- \frac{dU(r)}{dr} \frac{\vec{r}}{r}) = \frac{f(r)}{r} \; \underbrace{\vec{r} \times \vec{r}}_{=\vec{0}} = \vec{0} \end{equation} となる。同じ方向のベクトルの外積はゼロ。 つまり $\normalsize\displaystyle{f(r)}$ の関数形によらず, $\normalsize\displaystyle{\frac{d\vec{L}}{dt} =\vec{0}}$ が成り立つ。 よって $\normalsize\displaystyle{\vec{L}}$ は一定で角運動量が保存する。
角運動量が保存する場合,回転軸の向きも固定され,必然的に2次元平面内の運動になる
ところで角運動量が保存するってことは,回転がずっと続くという意味。
(例) 地球は太陽のまわりを,ずっと回っている。しかもその公転面は 2次元平面。これは万有引力が中心力ということの帰結。
- $\normalsize\displaystyle{(\frac{dx}{dt})(\frac{d^2 x}{dt^2})=\frac{1}{2}\frac{d}{dt} (\frac{dx}{dt})^2\;\;}$ ?
-
右辺を計算してみる。 \begin{eqnarray} \frac{1}{2}\frac{d}{dt} (\frac{dx}{dt})^2 &=& \frac{1}{2} \cdot 2 (\frac{dx}{dt})\cdot \frac{d}{dt} (\frac{dx}{dt})\nn\\ &=& (\frac{dx}{dt})(\frac{d^2 x}{dt^2}) \end{eqnarray} 以上。
同じような例: \begin{equation} f(x) =(ax+b)^2 \end{equation} みたいな $\normalsize\displaystyle{x}$ の関数を微分すると, \begin{eqnarray} \frac{d}{dx}f(x) &=&\frac{d}{dx}(ax+b)^2\nn\\ &=&2 (ax+b) \cdot \frac{d}{dx}(ax+b)\nn\\ &=& 2 (ax+b)\cdot a \end{eqnarray} となるので \begin{equation} (ax+b)\cdot a =\frac{1}{2}\frac{d}{dx}(ax+b)^2 \end{equation}
- 速度に比例する抵抗力( $\normalsize\displaystyle{-m\gamma v}$ ) になぜマイナスがつくの?
-
1. 物体の進行方向を正とすると,抵抗力は進行方向と逆向きの負なのでマイナスをつける。 これはわかりやすい。
2. 物体の進行方向を負とすると,抵抗力は進行方向と逆向きなのでマイナスは不要のはず? と思いきや,実際に速度に値を入れてみると,負の値が入るので,マイナスをつけないと, 現在進行中の負の方向に力,つまり推進力が働いてしまう。 マイナスをつけておくことで「マイナス $\normalsize\displaystyle{\times}$ 負の値=正の値」 となり,正の向き(進行方向と逆向き)の抵抗力になる。 よって,速度に比例する抵抗力を文字式で書いたときには $\normalsize\displaystyle{v}$ の前に必ず「マイナス」が必要。
- タイヤのふちに速度に比例する抵抗力が働くとどうなる?
-
回転の運動方程式 $\normalsize\displaystyle{I \alpha =\tau}$ を微分方程式で書く。 角速度を $\normalsize\displaystyle{\omega}$ すると, 条件より $\normalsize\displaystyle{\tau =-R \cdot k (R\omega)}$ , 角加速度は $\normalsize\displaystyle{\alpha =\frac{d\omega}{dt}}$ だから, \begin{equation} I \frac{d\omega}{dt} =-kR (R\omega) \end{equation} 円板の慣性モーメント \begin{equation} I =\frac{1}{2}mR^{2} \end{equation} を代入して整理すると \begin{equation} \frac{d\omega}{dt} = -\frac{2k}{m} \omega \end{equation} 両辺を $\normalsize\displaystyle{\frac{2k\omega}{m}}$ で割って, $\normalsize\displaystyle{t}$ 積分すると(順に式変形) \begin{equation} \frac{m}{2k} \int \frac{1}{\omega}\frac{d\omega}{dt} dt = -\int dt \end{equation} \begin{equation} \frac{m}{2k} \int \frac{1}{\omega} d \omega = - t +c \end{equation} \begin{equation} \frac{m}{2k} \ln \omega = - t +c \end{equation} よって \begin{equation} \omega= c' \exp(-\frac{2k}{m}t) \end{equation} が一般解。ここで $\normalsize\displaystyle{c'=\exp(\frac{2kc}{m})}$ も定数。
初期条件として $\normalsize\displaystyle{t=0}$ で $\normalsize\displaystyle{\omega=\omega_{0}}$ とすると $\normalsize\displaystyle{c'=\omega_{0}}$ となる。 したがって特殊解は \begin{equation} \omega= \omega_{0}\exp(-\frac{2k}{m}t) \end{equation} 回転角を $\normalsize\displaystyle{\theta}$ とすれば, \begin{equation} \omega=\frac{d\theta}{dt} \end{equation} なので,回転角は角速度を $\normalsize\displaystyle{t}$ 積分すれば求まる。 積分範囲はブレーキをかけた時点 $\normalsize\displaystyle{t=0}$ から止まるまでの $\normalsize\displaystyle{t=\infty}$ まで。 \begin{equation} \theta =\int_{0}^{\infty} \omega \, dt = \int_{0}^{\infty} \omega_{0}\exp(-\frac{2k}{m}t) \, dt = \omega_{0} (-\frac{m}{2k})(0-1)=\frac{m \omega_{0} }{2k} \end{equation} よって回転数は \begin{equation} N=\frac{\theta}{2\pi}= \frac{m \omega_{0} }{4\pi k} \end{equation}
- $\normalsize\displaystyle{\frac{dx}{dt} =f(x)g(t)}$ の形の微分方程式を解くには?
-
変数分離形の微分方程式。 両辺を $\normalsize\displaystyle{f(x)}$ で割って,両辺を $\normalsize\displaystyle{t}$ 積分すれば \begin{equation} \int \frac{1}{f(x)} \frac{dx}{dt} dt = \int g(t) dt +c \end{equation} つまり \begin{equation} \int \frac{1}{f(x)} dx = \int g(t) dt +c \end{equation} これが一般解。
(適用例) 物体に一定の力 $\normalsize\displaystyle{F}$ と速度に比例する抵抗力が働く場合の運動方程式 \begin{equation} m \frac{dv}{dt}= F - m \gamma v \end{equation} 変形すると \begin{equation} \frac{m}{F -m \gamma v} \frac{dv}{dt}=1 \end{equation} 両辺を $\normalsize\displaystyle{t}$ 積分すれば \begin{equation} \int \frac{m}{F -m \gamma v} dv = t +c \end{equation} よって \begin{equation} - \frac{1}{\gamma} \ln (F -m \gamma v) = t +c \end{equation} よって \begin{equation} \ln (F -m \gamma v) = -\gamma t +c \end{equation} よって \begin{equation} F -m \gamma v = c e^{-\gamma t} \end{equation} よって \begin{equation} v = \frac{F}{m \gamma} \left (1 +c e^{-\gamma t} \right ) \end{equation} (積分定数は任意なので式変形ではとことん $\normalsize\displaystyle{c}$ と置き直している)
- $\normalsize\displaystyle{\frac{dx}{dt} + P(t) x =Q(t)}$ の形の微分方程式を解くには?
-
(スライドでは説明しなかった方法:変数分離形でなくても適用可)
$\normalsize\displaystyle{P}$ と $\normalsize\displaystyle{Q}$ は $\normalsize\displaystyle{t}$ の関数とする(定数でもよい)。 方程式の両辺に $\normalsize\displaystyle{e^{\int P dt}}$ をかけると \begin{equation} \frac{dx}{dt} e^{\int P dt}+ P e^{\int P dt} x =Q e^{\int Pdt} \end{equation} すると左辺は \begin{equation} \frac{dx}{dt} e^{\int P dt}+ P e^{\int P dt} x =\frac{d}{dt} \left ( x e^{\int P dt} \right ) \end{equation} と書けるので,両辺を $\normalsize\displaystyle{t}$ で積分すれば \begin{equation} x e^{\int P dt} = \int Qe^{\int P dt} dt +c \end{equation} よって \begin{equation} x = e^{- \int P dt} \left (\int Q e^{\int P dt} dt +c\right ) \end{equation} これが一般解。
(適用例) 物体に一定の力 $\normalsize\displaystyle{F}$ と速度に比例する抵抗力が働く場合の運動方程式 \begin{equation} m \frac{dv}{dt}= F - m \gamma v \end{equation} 変形すると \begin{equation} \frac{dv}{dt} +\gamma v =\frac{F}{m} \end{equation} つまり $\normalsize\displaystyle{P=\gamma}$ , $\normalsize\displaystyle{Q=F/m}$ なので \begin{equation} \int P dt = \int \gamma dt =\gamma t \end{equation} \begin{equation} \int Q e^{\int P dt} dt = \int \frac{F}{m} e^{\gamma t} dt = \frac{F}{m \gamma} e^{\gamma t} \end{equation} よって \begin{eqnarray} v &=& e^{-\gamma t} \left ( \frac{F}{m \gamma} e^{\gamma t} +c\right )\nn\\ &=& \left ( \frac{F}{m \gamma} +c e^{-\gamma t} \right ) \nn\\ &=&\frac{F}{m \gamma} \left (1+ c e^{-\gamma t} \right ) \end{eqnarray} (積分定数は任意なので式変形ではとことん $\normalsize\displaystyle{c}$ と置き直している)
- テイラー展開が......。
-
以下,例を示す。グラフが重なっている領域は「より簡単な関数で代用できる」ということ。便利。 マクローリン展開と呼ぶこともある。
1. 三角関数(引数はradian) \begin{equation} \cos x=1-\frac{x^{2}}{2!} + \frac{x^{4}}{4!}- \frac{x^{6}}{6!}+\cdots \end{equation}
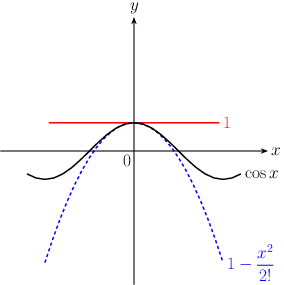
\begin{equation} \sin x=x-\frac{x^{3}}{3!} + \frac{x^{5}}{5!}- \frac{x^{7}}{7!}+\cdots \end{equation}
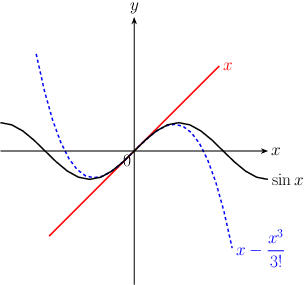
2. 指数・対数関数 \begin{equation} e^{x}=1 + x +\frac{x^{2}}{2!} + \frac{x^{3}}{3!} +\cdots \end{equation}
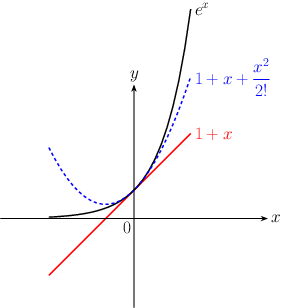
\begin{equation} \ln (1+ x)=x-\frac{x^{2}}{2} + \frac{x^{3}}{3}- \frac{x^{4}}{4}+\cdots \end{equation}
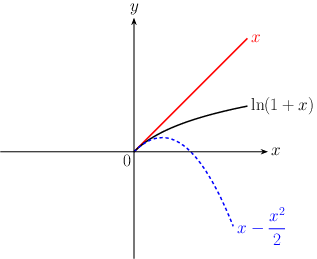
- 振り子でおもりが最下点にきたときのおもりの運動エネルギーは?
-
2通りの計算方法がある。両方から求めると検算になる。
1. 速度の特殊解を使って最下点にきたときの速度を求めて $\normalsize\displaystyle{K=\frac{1}{2}mv^{2}}$ に代入。
\begin{equation} \theta(t) =\theta_{0}\cos \sqrt{\frac{g}{l}} t \end{equation} より $\normalsize\displaystyle{\theta=0}$ となる 時刻 $\normalsize\displaystyle{t_{0}}$ は 例えば $\normalsize\displaystyle{\sqrt{\frac{g}{l}} t_{0} =\frac{\pi}{2}}$ より $\normalsize\displaystyle{t_{0}=\frac{\pi}{2} \sqrt{\frac{l}{g}}}$ (周期の $\normalsize\displaystyle{\frac{1}{4}}$ )
角速度は \begin{equation} \frac{d\theta}{dt}=-\sqrt{\frac{g}{l}}\theta_{0}\sin \sqrt{\frac{g}{l}} t \end{equation} だから,おもりの速さは \begin{equation} v(t)= l \frac{d\theta}{dt} = -l\sqrt{\frac{g}{l}}\theta_{0}\sin \sqrt{\frac{g}{l}} t \end{equation} これに $\normalsize\displaystyle{t=t_{0}}$ を代入すると \begin{equation} v( t_{0})= -l\sqrt{\frac{g}{l}}\theta_{0}\sin ( \sqrt{\frac{g}{l}} \cdot \frac{\pi}{2} \sqrt{\frac{l}{g}} )=-\sqrt{gl}\;\theta_{0} \end{equation} などなど(以上は $\normalsize\displaystyle{\theta_{0}\ll 1}$ の条件があってこそ)。2. 力学的エネルギー保存則から求める(位置エネルギーの最大値=運動エネルギーの最大値)。 保存則が使える理由はおもりに対して仕事をするのが重力のみだから。 おもりが最下点にきたときの位置エネルギーをゼロとするのが簡単。 \begin{equation} K+U=\frac{1}{2}mv^{2} +0 =0+mgl(1-\cos\theta_{0}) \end{equation} ここで $\normalsize\displaystyle{\theta_{0}\ll 1}$ より,テイラー展開の3次以上の項は無視すると \begin{equation} \cos\theta_{0} \simeq 1 -\frac{\theta_{0}^{2}}{2} \end{equation} などなど。
- 単振動の一般解の表式が何種類かあるのはどうして?
-
単振動の一般解として \begin{equation} x(t) =A \cos \omega t +B \sin \omega t \label{eqn:tanshindou1} \end{equation} \begin{equation} x(t) =a\,\cos (\omega t +\alpha) \label{eqn:tanshindou2} \end{equation} \begin{equation} x(t) =b \,\sin (\omega t +\beta) \label{eqn:tanshindou3} \end{equation} \begin{equation} x(t) =A' e^{i\omega t} +B' e^{-i\omega t} \label{eqn:tanshindou4} \end{equation} のような表し方があるのは,三角関数の合成や表し方に任意性があるから。 微分方程式に代入すると「左辺=右辺」をとなる。 つまり,すべて微分方程式 \begin{equation} \frac{d^{2}x}{dt^{2}}=-\omega^{2}x \end{equation} を満たす。 各表式の2つの任意定数はすべてつながっている。
(check) 式 \eqref{eqn:tanshindou2} は \begin{eqnarray} a\,\cos (\omega t +\alpha) &=& a\, (\cos \omega t \cos \alpha -\sin \omega t \sin\alpha) \nn\\ &=& a\cos \alpha \cos \omega t -a \sin\alpha\sin \omega t \end{eqnarray} と変形できるので, \begin{equation} a\cos \alpha=A\;,\quad -a \sin \alpha=B \quad \left ( a =\sqrt{A^{2}+B^{2}}\;,\quad \alpha =-\tan^{-1}\frac{B}{A} \right ) \end{equation} とおけば, \begin{equation} a\,\cos (\omega t +\alpha)=A \cos \omega t +B \sin \omega t \end{equation} となり,最初の式 \eqref{eqn:tanshindou1} になる。
(check) 式 \eqref{eqn:tanshindou3} は \begin{eqnarray} b\,\sin (\omega t +\beta) &=& b\, (\sin \omega t \cos \beta +\cos \omega t \sin\beta) \nn\\ &=& b\sin \beta \cos \omega t +b \cos\beta\sin \omega t \end{eqnarray} と変形できるので, \begin{equation} b\sin \beta=A\;,\quad b \cos\beta=B \quad \left ( b =\sqrt{A^{2}+B^{2}}\;,\quad \beta =\tan^{-1}\frac{A}{B} \right ) \end{equation} とおけば, \begin{equation} b\,\sin (\omega t +\beta)=A \cos \omega t +B \sin \omega t \end{equation} となり,最初の式 \eqref{eqn:tanshindou1} になる。
(check) 式 \eqref{eqn:tanshindou4} は \begin{eqnarray} A' e^{i\omega t} +B' e^{-i\omega t} &=& A' (\cos \omega t +i \sin \omega t)+B' (\cos \omega t -i \sin \omega t) \nn\\ &=& (A'+B')\cos \omega t +i(A' -B') \sin \omega t \end{eqnarray} と変形できるので, \begin{equation} A'+B' =A\;,\quad i(A' -B')=B \quad \left ( A' = \frac{A -iB}{2} \;,\quad B'=\frac{A +iB}{2} \right ) \end{equation} とおけば, \begin{equation} A' e^{i\omega t} +B' e^{-i\omega t} =A \cos \omega t +B \sin \omega t \end{equation} となり,最初の式 \eqref{eqn:tanshindou1} になる。
- 単振動の場合の力学的エネルギーはどのように書けるの?
-
例えば物体の変位が \begin{equation} x(t) =A \sin \omega t \end{equation} と表される運動は微分方程式 \begin{equation} \frac{d^{2}x}{dt^{2}} = -\omega^{2} x \end{equation} に従うので単振動。この式の両辺に物体の質量 $\normalsize\displaystyle{m}$ をかけると \begin{equation} m \frac{d^{2}x}{dt^{2}} = -m\omega^{2} x \end{equation} が運動方程式。 右辺の物体に働く力 $\normalsize\displaystyle{F = -m\omega^{2} x}$ は,位置エネルギー \begin{equation} U(x) = \frac{1}{2}m\omega^{2} x^{2} \end{equation} から \begin{equation} F = -\frac{dU}{dx} = -\frac{d}{dx} \left (\frac{1}{2}m\omega^{2} x^{2} \right ) = -m \omega^{2} x \end{equation} のように導かれる。よって力学的エネルギーは \begin{eqnarray} E&=& K +U \nn\\ &=& \frac{1}{2}m\left ( \frac{dx}{dt} \right )^{2} + \frac{1}{2}m\omega^{2} x^{2}\nn\\ &=& \frac{1}{2}m\left ( \omega A \cos \omega t \right )^{2} + \frac{1}{2}m\omega^{2} \left ( A \sin \omega t \right )^{2} \nn\\ &=& \frac{1}{2}m \omega^{2} A^{2} (\cos^{2} \omega t +\sin^{2} \omega t) \nn\\ &=& \frac{1}{2}m \omega^{2} A^{2} \end{eqnarray} と書ける。力学的エネルギーは時間に無関係となるのがポイント。 つまり,力学的エネルギー保存則が成立する。
- 減衰振動の特殊解はどの一般解から出発したら求まるの?
-
減衰振動の一般解も,単振動の一般解のときのように4通りくらいの表し方がある。 \begin{equation} x(t) =e^{-\gamma t} (A \cos \sqrt{\omega_0^2 -\gamma^2}\, t +B \sin \sqrt{\omega_0^2 -\gamma^2}\, t) \label{eqn:gensui1} \end{equation} \begin{equation} x(t) =a\, e^{-\gamma t} \cos (\sqrt{\omega_0^2 -\gamma^2}\, t +\alpha) \label{eqn:gensui2} \end{equation} \begin{equation} x(t) =b \,e^{-\gamma t} \sin (\sqrt{\omega_0^2 -\gamma^2}\, t +\beta) \label{eqn:gensui3} \end{equation} \begin{equation} x(t) =e^{-\gamma t} (A' e^{i \sqrt{\omega_0^2 -\gamma^2}\, t } +B' e^{-i \sqrt{\omega_0^2 -\gamma^2}\, t}) \label{eqn:gensui4} \end{equation} (Q「単振動の一般解の表式が何種類かあるのはどうして?」を参照)
初期条件を二つ課すと,二つの任意定数が定まり, 唯一の特殊解が求まる。 どの形式から出発しても,同じ関数形となる(見た目の表式は 三角関数の合成の仕方や表し方に応じて異なることがあるが, グラフを書くと同じとなる,重なる)。 演習課題の特殊解については一番目の式 \eqref{eqn:gensui1} から出発するのが比較的簡単。 式 \eqref{eqn:gensui1} を $\normalsize\displaystyle{t}$ で微分すると \begin{eqnarray} \frac{dx}{dt}&=&-\gamma e^{-\gamma t} (A \cos \sqrt{\omega_0^2 -\gamma^2}\, t +B \sin \sqrt{\omega_0^2 -\gamma^2}\, t)\nn\\ && + \sqrt{\omega_0^2 -\gamma^2}e^{-\gamma t} (-A \sin \sqrt{\omega_0^2 -\gamma^2}\, t +B \cos \sqrt{\omega_0^2 -\gamma^2}\, t) \end{eqnarray} よって \begin{eqnarray} \frac{dx}{dt}\biggr |_{t=0} = -\gamma A + \sqrt{\omega_0^2 -\gamma^2} B \end{eqnarray} 初速度が0の場合は,この式が0であるということ。よって \begin{equation} B=\frac{\gamma}{\sqrt{\omega_0^2 -\gamma^2} }A \end{equation} などなど。
- 双曲線関数とは?
-
指数関数を組み合わせた関数で,以下のように定義される。
1. ハイパボリックコサイン \begin{equation} \cosh x = \frac{e^{x}+e^{-x}}{2} \end{equation} グラフで表すと
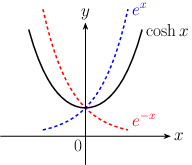
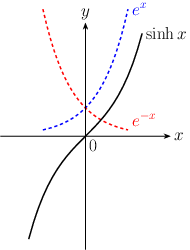
指数関数と $\normalsize\displaystyle{y}$ 軸の交点は $\normalsize\displaystyle{e^{0}=1}$ ,偶関数。2. ハイパボリックサイン \begin{equation} \sinh x = \frac{e^{x}-e^{-x}}{2} \end{equation} グラフで表すと
指数関数と $\normalsize\displaystyle{y}$ 軸の交点は $\normalsize\displaystyle{e^{0}=1}$ ,奇関数。3. ハイパボリックタンジェント \begin{equation} \tanh x = \frac{\sinh x}{\cosh x}= \frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \end{equation} グラフで表すと
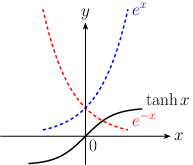
$\normalsize\displaystyle{x\to \infty}$ で $\normalsize\displaystyle{\tanh x \to 1}$ , $\normalsize\displaystyle{x\to -\infty}$ で $\normalsize\displaystyle{\tanh x \to -1}$ に収束,奇関数。
- 対数減衰度の求め方?
-
対数減衰度とは,減衰振動において1周期 \begin{equation} T= \frac{2\pi}{\sqrt{\omega_{0}^{2} -\gamma^{2}}} \end{equation} あたりでどれだけ振幅が減少するかを対数で表したもの。 時刻 $\normalsize\displaystyle{t}$ での変位を $\normalsize\displaystyle{x(t)}$ とすると \begin{equation} \delta = \ln x(t) -\ln x(t+T)=\ln \frac{x(t)}{x(t+T)} \end{equation} これに減衰振動の一般解(どれでもよい)を代入すると \begin{eqnarray} \delta &=& \ln \frac{x(t)}{x(t+T)} \nn\\ &=&\ln \frac{A e^{-\gamma t}\cos (\sqrt{\omega_{0}^{2} -\gamma^{2}} t +\alpha)} {A e^{-\gamma (t+T)}\cos (\sqrt{\omega_{0}^{2} -\gamma^{2}} (t+T) +\alpha)}\nn\\ &=& \ln \frac{A e^{-\gamma t}\cos (\sqrt{\omega_{0}^{2} -\gamma^{2}} t +\alpha)} {A e^{-\gamma (t+T)}\cos (\sqrt{\omega_{0}^{2} -\gamma^{2}} t +\alpha)}\quad \mbox{(この変形がポイント!)}\nn\\ &=& \ln \frac{e^{-\gamma t}}{ e^{-\gamma (t+T)}}\nn\\ &=& \ln e^{\gamma T} \nn\\ &=& \gamma T\nn\\ &=& \frac{2\pi\gamma }{\sqrt{\omega_{0}^{2} -\gamma^{2}}}\quad \fbox{答え} \end{eqnarray}
- 強制振動で共振がおこる条件では運動はどうなる?
-
微分方程式が \begin{equation} m\frac{d^{2}x}{dt^{2}} =-m\omega_{0}^{2}x +F_{0}\cos \omega t \end{equation} で与えられる場合で $\normalsize\displaystyle{\omega \to \omega_{0}}$ とするとどうなるかを見れば良い。 この微分方程式の一般解は \begin{equation} x(t)= A\cos \omega_{0}t +B \sin \omega_{0}t +\frac{F_{0}}{m(\omega_{0}^{2}-\omega^{2})} \cos \omega t \end{equation} で $\normalsize\displaystyle{\omega \to \omega_{0}}$ とすれば第3項目の分数の分母が $\normalsize\displaystyle{\omega_{0}^{2}-\omega^{2} \to 0}$ となるので $\normalsize\displaystyle{|x| \to \infty}$ となる。 どのように $\normalsize\displaystyle{|x| \to \infty}$ となるかを知りたければ,初期条件を課した特殊解の振る舞いを調べればよい。
たとえば,初期条件として $\normalsize\displaystyle{t=0}$ で $\normalsize\displaystyle{x=0}$ , $\normalsize\displaystyle{\frac{dx}{dt}=0}$ (まったくの静止状態からスタート) とすると \begin{equation} x(0)= A+\frac{F_{0}}{m(\omega_{0}^{2}-\omega^{2})} =0 \end{equation} より \begin{equation} A = -\frac{F_{0}}{m(\omega_{0}^{2}-\omega^{2})} \end{equation} また, \begin{equation} \frac{dx}{dt} \biggr |_{t=0} = B\omega_{0} =0 \end{equation} より \begin{equation} B=0 \end{equation} よって特殊解は \begin{equation} x(t)= \frac{F_{0}}{m(\omega_{0}^{2}-\omega^{2})} ( \cos \omega t - \cos \omega_{0} t ) \end{equation} この式で $\normalsize\displaystyle{\omega \to \omega_{0}}$ とすると 分母・分子ともに $\normalsize\displaystyle{0}$ に近くので「ロピタルの定理」を 使って(分母・分子をそれぞれ $\normalsize\displaystyle{\omega}$ で 微分して $\normalsize\displaystyle{\omega \to \omega_{0}}$ とする)その極限を見ると \begin{equation} x(t) = \frac{F_{0}}{2m\omega_{0}} t \sin \omega_{0} t \end{equation} つまり,振幅が時間に比例して大きくなる振動運動となる。
- 単振動+減衰振動+強制振動の特殊解の求め方って色々あるの?
-
1. 普通に解く。
微分方程式 \begin{equation} \frac{d^{2}x}{dt^{2}} + 2\gamma\frac{dx}{dt} + \omega_{0}^{2}x =\frac{F_{0}}{m}\sin \omega t \end{equation} に $\normalsize\displaystyle{x(t)=A\sin (\omega t -\delta)}$ を代入すると \begin{eqnarray} &&(\omega_{0}^{2}-\omega^{2})A(\cos\delta\sin \omega t -\sin\delta\cos \omega t )\nn\\ && + 2\gamma \omega A ( \cos\delta \cos \omega t +\sin\delta \sin \omega t ) - \frac{F_{0}}{m}\sin \omega t =0 \end{eqnarray} 整理すると \begin{eqnarray} && \left \{ (\omega_{0}^{2}-\omega^{2})A\cos\delta +2\gamma \omega A\sin\delta -\frac{F_{0}}{m} \right \} \sin \omega t \nn\\ &&+\left \{ -(\omega_{0}^{2}-\omega^{2})A\sin\delta +2\gamma \omega A\cos\delta \right \} \cos\omega t=0 \end{eqnarray} つまり \begin{equation} f_{1}(A,\delta) = (\omega_{0}^{2}-\omega^{2})A\cos\delta +2\gamma \omega A\sin\delta -\frac{F_{0}}{m}=0 \end{equation} \begin{equation} f_{2}(A,\delta) = -(\omega_{0}^{2}-\omega^{2})A\sin\delta +2\gamma \omega A\cos\delta =0 \end{equation} まず, $\normalsize\displaystyle{f_{2}(A,\delta)=0}$ より \begin{equation} \tan\delta =\frac{\sin \delta}{\cos\delta}=\frac{2\gamma \omega}{\omega_{0}^{2}-\omega^{2}} \quad\quad ( \delta =\tan^{-1}\frac{2\gamma \omega}{\omega_{0}^{2}-\omega^{2}} ) \end{equation} これより \begin{equation} \cos\delta = \frac{\omega_{0}^{2}-\omega^{2}}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2} +(2\gamma\omega)^{2}}} \end{equation} \begin{equation} \sin \delta = \frac{2\gamma\omega}{\sqrt{(\omega_{0}^{2}-\omega^{2})^{2} +(2\gamma \omega)^{2}}} \end{equation} 次に, $\normalsize\displaystyle{f_{1}(A,\delta)=0}$ より \begin{equation} A\left \{ (\omega_{0}^{2}-\omega^{2})\cos\delta +2\gamma\omega \sin\delta \right \}=\frac{F_{0}}{m} \end{equation} これに $\normalsize\displaystyle{\cos \delta}$ , $\normalsize\displaystyle{\sin \delta}$ を代入すると \begin{equation} A \sqrt{(\omega_{0}^{2}-\omega^{2})^{2} +(2\gamma\omega)^{2}} =\frac{F_{0}}{m} \end{equation} よって \begin{equation} A=\frac{F_{0}}{m\sqrt{(\omega_0^2 -\omega^2)^2 +4 \gamma^2 \omega^2}} \end{equation} を得る。これをはじめに仮定した解に戻せば特殊解。2. 複素数の方法で解く。
$\normalsize\displaystyle{x \to z=x+iy\in \mathbb{C}}$ として 変位を複素数に拡張。あわせて振動的外力もオイラーの公式を使って拡張。 \begin{equation} \frac{d^{2}z}{dt^{2}} + 2\gamma\frac{dz}{dt} + \omega_{0}^{2}z =\frac{F_{0}}{m}e^{i\omega t} \end{equation} この方程式を $\normalsize\displaystyle{z}$ について解き,虚部を抽出すればそれが本来解くべき方程式の解(外力が $\normalsize\displaystyle{\sin}$ だから)。 $\normalsize\displaystyle{z =z_{0}e^{i\omega t}}$ を代入すると \begin{equation} \{ (\omega_{0}^{2}-\omega^{2} ) + i (2 \gamma \omega ) \} z_{0} e^{i\omega t} = \frac{F_{0}}{m}e^{i\omega t} \end{equation} $\normalsize\displaystyle{z_{0}}$ について解くと \begin{equation} z_{0} =\frac{F_{0}}{m}\frac{1}{(\omega_{0}^{2}-\omega^{2} ) + i (2 \gamma \omega ) } =\frac{F_{0}}{m}\frac{(\omega_{0}^{2}-\omega^{2} ) - i (2 \gamma \omega ) }{(\omega_{0}^{2}-\omega^{2} )^{2} + (2 \gamma \omega )^{2} } \end{equation} ここで複素数の極座標表示 \begin{equation} z =x+iy =\sqrt{x^{2}+y^{2}} \; e^{i\delta} \; , \quad \tan \delta = \frac{y}{x} \end{equation} との対応から \begin{equation} z_{0} = \frac{F_{0}}{m}\frac{\sqrt{ (\omega_{0}^{2}-\omega^{2} )^{2} + (2 \gamma \omega )^{2}}\; e^{-i \delta}}{(\omega_{0}^{2}-\omega^{2} )^{2} + (2 \gamma \omega )^{2} } = \frac{F_{0}}{m\sqrt{ (\omega_{0}^{2}-\omega^{2} )^{2} + (2 \gamma \omega )^{2}} }\; e^{-i \delta} \end{equation} ただし \begin{equation} \tan \delta = \frac{2 \gamma \omega}{\omega_{0}^{2}-\omega^{2}} \end{equation} 以上より \begin{eqnarray} z &=& z_{0}e^{i\omega t} \nn\\ &=&\frac{F_{0}}{m\sqrt{ (\omega_{0}^{2}-\omega^{2} )^{2} + (2 \gamma \omega )^{2}} }e^{-i \delta} e^{i\omega t}\nn\\ &=&\frac{F_{0}}{m\sqrt{ (\omega_{0}^{2}-\omega^{2} )^{2} + (2 \gamma \omega )^{2}} }e^{i (\omega t -\delta)} \end{eqnarray} 虚部は普通に解いたものと一致( $\normalsize\displaystyle{e^{i (\omega t -\delta)}=\cos (\omega t -\delta) +i\sin (\omega t -\delta)}$ )。3. ラプラス変換で解く。
\begin{equation} F(s)=\mathcal{L}(f)=\int_{0}^{\infty}e^{-st}f(t) dt \end{equation} を関数 $\normalsize\displaystyle{f(t)}$ のラプラス変換という。 見たことのない人のためにいくつか準備。 \begin{eqnarray} \mathcal{L}(\cos\omega t)+i\mathcal{L}(\sin \omega t) &=& \mathcal{L}(\cos\omega t+i\sin \omega t)\nn\\ &=& \mathcal{L}( e^{i\omega t}) \nn\\ &=& \int_{0}^{\infty}e^{-st} e^{i\omega t} dt \nn\\ &=& \int_{0}^{\infty}e^{(i\omega -s)t} dt \nn\\ &=& [\frac{1}{i\omega -s}e^{(i\omega -s)t}]_{0}^{\infty}\nn\\ &=& \frac{1}{s-i\omega}\nn\\ &=& \frac{s}{s^{2}+\omega^{2}}+i \frac{\omega}{s^{2}+\omega^{2}} \end{eqnarray} より \begin{equation} \mathcal{L}(\cos\omega t)=\frac{s}{s^{2}+\omega^{2}}\;,\quad \mathcal{L}(\sin \omega t)=\frac{\omega}{s^{2}+\omega^{2}} \end{equation} また \begin{eqnarray} \mathcal{L}( \dot{x} ) &=&\int_{0}^{\infty}e^{-st} \dot{x} dt \nn\\ &=& [e^{-st} x]_{0}^{\infty} +s \int_{0}^{\infty}e^{-st} x dt \nn\\ &=& - x(0) +s \mathcal{L}(x) \end{eqnarray} 加えて \begin{eqnarray} \mathcal{L}( \ddot{x} ) &=&\int_{0}^{\infty}e^{-st} \ddot{x} dt \nn\\ &=& [e^{-st} \dot{x}]_{0}^{\infty} +s \int_{0}^{\infty}e^{-st} \dot{x}dt \nn\\ &=& - \dot{x}(0) +s \mathcal{L}(\dot{x})\nn\\ &=& - \dot{x}(0) +s (- x(0) +s \mathcal{L}(x))\nn\\ &=& s^{2} \mathcal{L}(x)-sx(0) -\dot{x}(0) \end{eqnarray} ここまで準備した上で微分方程式 \begin{equation} \frac{d^{2}x}{dt^{2}} + 2\gamma\frac{dx}{dt} + \omega_{0}^{2}x =\frac{F_{0}}{m}\sin \omega t \end{equation} の両辺をラプラス変換すると \begin{equation} s^{2} \mathcal{L}(x)-sx(0) -\dot{x}(0) + 2\gamma ( - x(0) +s \mathcal{L}(x)) + \omega_{0}^{2}\mathcal{L}(x) = \frac{F_{0}}{m} \mathcal{L}(\sin \omega t) \end{equation} 整理すると \begin{equation} (s^{2} +2\gamma s +\omega_{0}^{2} )\mathcal{L}(x) =(s + 2\gamma ) x(0) +\dot{x}(0) + \frac{F_{0}}{m} \frac{\omega}{s^{2}+\omega^{2}} \end{equation} あとは逆変換あるのみ。 \begin{eqnarray} \mathcal{L}(x) &=& \underbrace{\frac{(s + 2\gamma ) x(0) +\dot{x}(0)}{ s^{2} +2\gamma s +\omega_{0}^{2} }}_{\mathcal{L}(x_{g})} + \underbrace{\frac{F_{0}\omega}{m(s^{2}+\omega^{2}) ( s^{2} +2\gamma s +\omega_{0}^{2} )} }_{\mathcal{L}(x_{s})} \end{eqnarray} ここで \begin{equation} s^{2} +2\gamma s +\omega_{0}^{2} = (s+\gamma)^{2}+\omega_{0}^{2}-\gamma^{2} \end{equation} $\normalsize\displaystyle{\mathcal{L}(x_{g})}$ の逆変換は \begin{eqnarray} x_{g}&=& \mathcal{L}^{-1}\{ \frac{(s +2\gamma ) x(0) +\dot{x}(0)}{ s^{2} +2\gamma s +\omega_{0}^{2} } \} \nn\\ &=& \mathcal{L}^{-1}\{ \frac{(s + \gamma ) x(0)} { (s+\gamma)^{2}+\omega_{0}^{2}-\gamma^{2} } +\frac{\gamma x(0) +\dot{x}(0)}{ (s+\gamma)^{2}+\omega_{0}^{2}-\gamma^{2} } \} \nn\\ &=& \mbox{中略!}\nn\\ &=& e^{-\gamma t}\left [ x(0) \cos \sqrt{\omega_{0}^{2}-\gamma^{2}} \; t + \frac{\gamma x(0) +\dot{x}(0)}{\sqrt{\omega_{0}^{2}-\gamma^{2}}}\sin \sqrt{\omega_{0}^{2}-\gamma^{2}} \;t \right ] \end{eqnarray} これが同次方程式の解。例えば,初期条件を $\normalsize\displaystyle{x(0)=x_{0}}$ , $\normalsize\displaystyle{\dot{x}(0)=0}$ のように具体的に与えると \begin{equation} x_{g} =x_{0} e^{-\gamma t}\left [ \cos \sqrt{\omega_{0}^{2}-\gamma^{2}} \; t + \frac{\gamma }{\sqrt{\omega_{0}^{2}-\gamma^{2}}}\sin \sqrt{\omega_{0}^{2}-\gamma^{2}} \;t \right ] \end{equation} のような減衰振動の特殊解(演習問題の答え)になる。$\normalsize\displaystyle{\mathcal{L}(x_{s})}$ の逆変換は \begin{eqnarray} x_{s}&=& \mathcal{L}^{-1}\{ \frac{F_{0}\omega}{m(s^{2}+\omega^{2}) ( s^{2} +2\gamma s +\omega_{0}^{2} )} \} \nn\\ &=& \mbox{中略!!!}\nn\\ &=& \frac{F_{0}}{m} \frac{1}{( \omega_{0}^{2} - \omega^{2} )^{2} +4 \gamma^{2} \omega^{2}} [ ( \omega_{0}^{2} - \omega^{2} ) \sin \omega t -2\gamma \omega \cos \omega t \nn\\ && + e^{-\gamma t}( 2\gamma \omega \cos \sqrt{\omega_{0}^{2}-\gamma^{2}} t + \frac{ \omega ( \omega^{2} - \omega_{0}^{2} +2\gamma^{2})}{\sqrt{\omega_{0}^{2}-\gamma^{2}}} \sin \sqrt{\omega_{0}^{2}-\gamma^{2}} t ) ]\nn\\ &=& \frac{F_{0}}{m\sqrt{(\omega_0^2 -\omega^2)^2 +4 \gamma^2 \omega^2}} \sin (\omega t -\delta )\nn\\ &&+ \frac{F_{0} e^{-\gamma t}}{m (( \omega_{0}^{2} - \omega^{2} )^{2} +4 \gamma^{2} \omega^{2})} ( 2\gamma \omega \cos \sqrt{\omega_{0}^{2}-\gamma^{2}} t + \frac{ \omega ( \omega^{2} - \omega_{0}^{2} +2\gamma^{2})}{\sqrt{\omega_{0}^{2}-\gamma^{2}}} \sin \sqrt{\omega_{0}^{2}-\gamma^{2}} t ) \end{eqnarray} 第1項目は上に書いてあるのと当然同じ。 第2項目は $\normalsize\displaystyle{x =A\sin (\omega t-\delta)}$ を代入する発見的方法では見つからない解。 しかしラプラス変換にかかるとあぶり出される。 時間が経過すると第1項目だけが残る。 文献やインターネットを調べた限りでは どこにも第2項目のことは載っていないので私が自称発見者。 そもそも,第2項目がないと全体の解 $\normalsize\displaystyle{x=x_{g}+x_{s}}$ として,初期条件を満たせなくなる。 結構計算が面倒だった。 よって名前をつけるならば駒の解。細かい?
- $\normalsize\displaystyle{f(\omega^{2})=(\omega_{0}^{2}-\omega^{2})^{2}+4\gamma^{2}\omega^{2}}$ の極値は?
-
$\normalsize\displaystyle{\omega^{2}=x}$ とおけば \begin{equation} f(x) =(\omega_{0}^{2}-x)^{2}+4\gamma^{2}x \end{equation} は $\normalsize\displaystyle{x}$ についての2次関数。よって極値は一つ。 展開すると $\normalsize\displaystyle{x^{2}}$ の前の係数は正なので, その極値は最小値。 極値では一階の導関数(関数の接線の傾き)がゼロなので \begin{equation} \frac{df}{dx}=2 (\omega_{0}^{2}-x)(-1) +4 \gamma^{2} =0 \end{equation} これを $\normalsize\displaystyle{x}$ について解くと \begin{equation} x = \omega_{0}^{2} -2\gamma^{2} \equiv X \end{equation} よって \begin{equation} \omega =\sqrt{X} = \sqrt{\omega_{0}^{2} -2\gamma^{2}} \end{equation} で最小値をとる。振幅の分母が最小になるということは振幅は最大になる。 つまり共振がおこる。よってこの $\normalsize\displaystyle{\omega}$ が共振角振動数。 この関数の最小値は \begin{eqnarray} f (X)&=& (\omega_{0}^{2}-X)^{2}+4\gamma^{2}X \nn\\ &=&(\omega_{0}^{2}-(\omega_{0}^{2} -2\gamma^{2}))^{2}+4\gamma^{2}(\omega_{0}^{2} -2\gamma^{2})\nn\\ &=& (2 \gamma^{2})^{2} + 4\gamma^{2}(\omega_{0}^{2} -2\gamma^{2}) \nn\\ &=&4\gamma^{2}(\omega_{0}^{2} -\gamma^{2}) \end{eqnarray} なお,2次関数の極値は平方完成によっても求まる。 \begin{eqnarray} f(x)&=& x^{2}+2 (2\gamma^{2} - \omega_{0}^{2})x +\omega_{0}^{4} \nn\\ &=& (x + 2\gamma^{2} - \omega_{0}^{2})^{2} - (2\gamma^{2} - \omega_{0}^{2})^{2 }+\omega_{0}^{4}\nn\\ &=& (x - ( \omega_{0}^{2}- 2\gamma^{2} ) )^{2} + 4\gamma^{2}(\omega_{0}^{2} -\gamma^{2}) \end{eqnarray} これより極値は $\normalsize\displaystyle{x = \omega_{0}^{2}- 2\gamma^{2}}$ のときで,その値は $\normalsize\displaystyle{4\gamma^{2}(\omega_{0}^{2} -\gamma^{2})}$
- 共振時の最大振幅は?
-
先に求めた共振角振動数 \begin{equation} \omega = \sqrt{\omega_{0}^{2} -2\gamma^{2}} \end{equation} を振幅 \begin{equation} A=\frac{F_{0}}{m\sqrt{(\omega_0^2 -\omega^2)^2 +4 \gamma^2 \omega^2}} \end{equation} に代入するだけ。
- RLC回路とは?
-
抵抗R,インダクタL (コイル),コンデンサCを直列または並列接続した回路のこと。 起電力として直流電源,交流電源がある。 直列で交流電源をつないだ回路の方程式が,力学の単振動と速度に比例する抵抗力と振動的外力 が働く場合の力学系の方程式と同じ形をしている。よって 力学系と同様に,共振が起こり得る。 回路の方は,この共振を利用して,回路のインピーダンス(交流抵抗)を大きく変化させる。 例えばラジオでは,このような性質を利用して電波の受信をする(ただし並列回路)。 ふたつの方程式を比較できるように並べてみる。
力学系 \begin{equation} m\frac{d^{2}x}{dt^{2}}=-m\omega_{0}^{2}x -2m\gamma\frac{dx}{dt} +F_{0}\sin \omega t \end{equation} RLC回路 \begin{equation} L \frac{d^{2}I}{dt^{2}} =-\frac{1}{C}I -R \frac{dI}{dt} +\omega \phi_{0} \cos \omega t \end{equation} ここで外力は初期位相次第で同じ三角関数になる。 質量 $\normalsize\displaystyle{m}$ と インダクタンス $\normalsize\displaystyle{L}$ , 復元力のばね定数 $\normalsize\displaystyle{m\omega_{0}^{2}}$ と 静電容量の逆数 $\normalsize\displaystyle{C^{-1}}$ , 抵抗係数 $\normalsize\displaystyle{2m\gamma}$ と 抵抗 $\normalsize\displaystyle{R}$ , そして,変位 $\normalsize\displaystyle{x}$ と電流 $\normalsize\displaystyle{I}$ を対応させれば, 同じタイプの方程式になっていることがわかる。 コンデンサは力学の観点ではばねと同じ。 力学系のほうの特殊解がわかっていれば,その中の文字を入れ替えれば 回路の方程式の特殊解が直ちに得られる。 上の比較より \begin{equation} x \to I \end{equation} \begin{equation} L \to m \end{equation} \begin{equation} m\omega_{0}^{2} \to \frac{1}{C} \end{equation} \begin{equation} 2m\gamma \to R \end{equation} \begin{equation} F_{0} \to \omega \phi_{0} \end{equation} の対応があることがわかる( $\normalsize\displaystyle{\sin}$ と $\normalsize\displaystyle{\cos}$ の対応は位相だけの問題なので振幅には無関係)。 よって特殊解の振幅は \begin{eqnarray} \frac{F_{0}}{m\sqrt{ (\omega_{0}^{2} -\omega^{2})^{2} +4\gamma^{2} \omega^{2}}} &\to& \frac{\omega \phi_{0}}{L \sqrt{ (\frac{1}{LC}-\omega^{2} )^{2} +4 (\frac{R}{2L})^{2} \omega^{2} }}\nn\\ &=& \frac{ \phi_{0}}{ \sqrt{ (\frac{1}{\omega C}- \omega L )^{2} +R^{2} }} \end{eqnarray} よって \begin{equation} \frac{1}{\omega C}- \omega L= 0 \end{equation} を満たす角振動数,つまり \begin{equation} \omega = \sqrt{\frac{1}{LC}} \end{equation} で共振が起こる(分母が最小)。 ちなみに上の関係を, \begin{equation} Z= \sqrt{ (\frac{1}{\omega C}- \omega L )^{2} +R^{2} } \end{equation} として $\normalsize\displaystyle{\phi_{0} =ZI}$ と書くと,これは交流の場合のオームの法則になっている。 この $\normalsize\displaystyle{Z}$ を交流抵抗(インピーダンス)という。 共振のときは $\normalsize\displaystyle{\phi_{0} =RI}$ で抵抗が最小となって電流がたくさん流れる。 対応関係を用いない場合は直接,微分方程式を解けば良い。 「Q.単振動+減衰振動+強制振動の特殊解の求め方って色々あるの? 」を参照。 当然,同じ結果になる。
- 太陽からみた地球の速さは?
-
面積速度を $\normalsize\displaystyle{v_{a}}$ (aはareaの意味),楕円軌道の接線方向の速さを $\normalsize\displaystyle{v}$ ,太陽と地球の間の距離を $\normalsize\displaystyle{r}$ とすると \begin{equation} v_{a} =\frac{1}{2} r (r\dot{\theta}) = \frac{1}{2} r v \end{equation} 万有引力のような中心力の場合は $\normalsize\displaystyle{v_{a}=}$ 一定。 $\normalsize\displaystyle{\dot{\theta}}$ は角速度。 よって半径 $\normalsize\displaystyle{r}$ のときの接線方向のときは \begin{equation} v= \frac{2v_{a}}{r} \end{equation} つまり距離 $\normalsize\displaystyle{r}$ の大小によって遅くなったり速くなったりする。 $\normalsize\displaystyle{r}$ が最小のときは $\normalsize\displaystyle{v}$ が最大。逆に $\normalsize\displaystyle{r}$ が最大のときは $\normalsize\displaystyle{v}$ が最小。
- 静止した2物体間に万有引力のみが働くとどうなる?
-
時刻 $\normalsize\displaystyle{t}$ における質点間の 距離を $\normalsize\displaystyle{x(t)}$ とすると,運動方程式は \begin{equation} \mu \frac{d^{2}x}{dt^{2}} =- \frac{GM\mu}{x^{2}} \end{equation} ここで $\normalsize\displaystyle{M=m_{1}+m_{2}}$ は重心質量, $\normalsize\displaystyle{\mu=\frac{m_{1}m_{2}}{m_{1}+ m_{2}} =\frac{m_{1}m_{2}}{M}}$ は換算質量。 この微分方程式を $\normalsize\displaystyle{t=0}$ で $\normalsize\displaystyle{x =R}$ , $\normalsize\displaystyle{\frac{dx}{dt}=0}$ の条件で解く。 両辺に $\normalsize\displaystyle{dx/dt}$ をかけて $\normalsize\displaystyle{\frac{dx}{dt}\frac{d^{2}x}{dt^{2}} = - \frac{GM}{x^{2}}\frac{dx}{dt}}$ , 変形して $\normalsize\displaystyle{\frac{1}{2}\frac{d}{dt}\left ( \frac{dx}{dt}\right )^{2}=\frac{d}{dt}\frac{GM}{x}}$ , 両辺を $\normalsize\displaystyle{t}$ で積分して \begin{equation} \frac{dx}{dt} = -\sqrt{2GM} \sqrt{\frac{1}{x}-\frac{1}{R}} \end{equation} を得る(初期条件を考慮)。 マイナス符号は速度の方向を表す。
すると,以下の時間が経過すると接触する。 \begin{eqnarray} T&=& \int_{0}^{T}dt\nn\\ &=& -\frac{1}{\sqrt{2GM}} \int_{R}^{0} \sqrt{\frac{Rx}{R-x}}dx \nn\\ &=& \mbox{中略!}\nn\\ &=&\frac{\pi}{2}\sqrt{\frac{R^{3}}{2GM}} \end{eqnarray} 途中,置換積分とかで計算できる。 $\normalsize\displaystyle{\beta}$ 関数とか $\normalsize\displaystyle{\gamma}$ 関数とか知っていると積分は簡単。 知らなければこれを機に調べるというのもあり。最初に相対角運動量がある場合は2次曲線的な運動になる。接触しない。